گرادیان برداری در یادگیری ماشین

گرادیان برداری چیست؟ اگر تا به حال حساب دیفرانسیل و انتگرال یا فیزیک خوانده اید، ممکن است با این اصطلاح برخورد کرده باشید. بردار گرادیان یک مفهوم ریاضی است که برای توصیف نرخ تغییر یک تابع استفاده می شود.

این یک ابزار مهم در بسیاری از زمینه‌های علم و مهندسی است، زیرا به ما امکان می‌دهد بفهمیم که یک تابع در جهات مختلف چگونه رفتار می‌کند.

برای درک مفهوم بردار گرادیان، اجازه دهید با یک مثال ساده شروع کنیم.

گرادیان برداری چیست؟

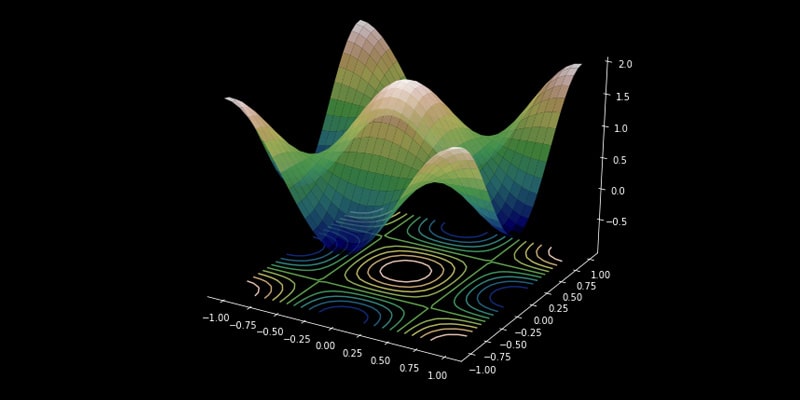
تصور کنید روی تپه ای ایستاده اید و می خواهید بدانید کدام جهت شیب دارترین است.

می توانید به اطراف نگاه کنید و ببینید که زمین به کدام سمت شیب بیشتری دارد.

بردار گرادیان مانند نسخه ریاضی این ایده است.

جهت تندترین شیب یک تابع در یک نقطه مشخص را به ما می گوید.

از نظر ریاضی، بردار گرادیان برداری است که در جهت بیشترین میزان افزایش یک تابع است.

با نماد ∇ (تلفظ “del”) و سپس تابع نشان داده می شود.

برای مثال، اگر تابع f(x,y) داشته باشیم، بردار گرادیان به صورت ∇f(x,y) نوشته می شود.

بردار گرادیان هم قدر و هم جهت دارد.

بزرگی بردار گرادیان نشان‌دهنده نرخ تغییر تابع است، در حالی که جهت نشان‌دهنده جهت تندترین شیب است.

اگر بزرگی بردار گرادیان بزرگ باشد، به این معنی است که تابع به سرعت در حال تغییر است.

اگر قدر کوچک باشد، به این معنی است که تابع به آرامی در حال تغییر است.

برای محاسبه بردار گرادیان، باید مشتقات جزئی تابع را با توجه به هر متغیر بگیریم.

به عنوان مثال، اگر تابع f(x, y) داشته باشیم، مشتق جزئی f را نسبت به x (∂f/∂x) و مشتق جزئی f را با توجه به y (∂f/∂y) محاسبه می کنیم.).

این مشتقات جزئی به ترتیب نشان دهنده نرخ تغییر تابع در جهت x و y هستند.

هنگامی که مشتقات جزئی را محاسبه کردیم، می توانیم آنها را ترکیب کنیم تا بردار گرادیان را تشکیل دهیم.

جزء x بردار گرادیان برابر با مشتق جزئی نسبت به x (∂f/∂x) و جزء y برابر با مشتق جزئی نسبت به y (∂f/∂y) است.

بنابراین، بردار گرادیان ∇f(x، y) با (∂f/∂x، ∂f/∂y) داده می شود.

بردار گرادیان را می توان به روش های مختلفی استفاده کرد.

به عنوان مثال، در فیزیک، از آن برای توصیف میدان الکتریکی اطراف یک ذره باردار استفاده می شود.

در اقتصاد، برای توصیف نرخ تغییر تابع مطلوبیت استفاده می شود.

در گرافیک کامپیوتری، از آن برای ایجاد جلوه های نورپردازی واقعی استفاده می شود.

در نتیجه، بردار گرادیان یک مفهوم ریاضی است که برای توصیف نرخ تغییر یک تابع استفاده می شود.

جهت تندترین شیب تابع در یک نقطه مشخص را به ما می گوید.

با محاسبه مشتقات جزئی تابع، می توان مقدار و جهت بردار گرادیان را تعیین کرد.

بردار گرادیان ابزار قدرتمندی است که در بسیاری از زمینه های علوم و مهندسی برای درک نحوه رفتار توابع در جهات مختلف استفاده می شود.

کاربردهای بردار گرادیان در ریاضیات

بردار گرادیان یک مفهوم ریاضی است که به طور گسترده در زمینه های مختلف از جمله ریاضیات استفاده می شود.

برداری است که در جهت شیب زیاد یک تابع در یک نقطه مشخص است.

به عبارت دیگر، جهتی را که یک تابع سریعترین افزایش می یابد به ما می گوید.

یکی از کاربردهای اصلی بردار گرادیان در ریاضیات در مسائل بهینه سازی است.

بهینه سازی فرآیند یافتن حداکثر یا حداقل مقدار یک تابع است.

بردار گرادیان با ارائه اطلاعاتی در مورد جهتی که باید برای رسیدن به نقطه حداکثر یا حداقل به ما در این فرآیند کمک کند.

به عنوان مثال، فرض کنید تابعی داریم که نشان دهنده سود یک شرکت بر اساس تعداد واحدهای فروخته شده است.

ما می خواهیم تعداد واحدهایی را پیدا کنیم که سود را به حداکثر می رساند.

با گرفتن بردار گرادیان تابع سود در یک نقطه معین، می‌توانیم جهتی را که در آن سود سریع‌ترین افزایش می‌یابد تعیین کنیم.

این اطلاعات به ما اجازه می دهد تا تعداد واحدهای فروخته شده را متناسب با آن تنظیم کنیم تا سود را به حداکثر برسانیم.

یکی دیگر از کاربردهای بردار گرادیان در زمینه فیزیک، به ویژه در مطالعه میدان های برداری است.

فیلد برداری تابعی است که به هر نقطه از فضا یک بردار اختصاص می دهد.

بردار گرادیان یک تابع اسکالر یک میدان برداری است که جهت و بزرگی حداکثر نرخ تغییر تابع اسکالر را در هر نقطه نشان می دهد.

در فیزیک، میدان های برداری برای توصیف پدیده های فیزیکی مختلف مانند جریان سیالات یا توزیع میدان های الکتریکی استفاده می شود.

بردار گرادیان با ارائه اطلاعاتی در مورد جهت و بزرگی تغییراتی که در هر نقطه از فضا رخ می دهد به ما کمک می کند تا این پدیده ها را درک کنیم.

بردار گرادیان علاوه بر بهینه سازی و فیزیک، در سایر زمینه های ریاضیات مانند هندسه دیفرانسیل و حساب دیفرانسیل و انتگرال نیز کاربرد دارد.

در هندسه دیفرانسیل، بردار گرادیان برای تعریف مفهوم بردار مماس بر سطح استفاده می شود.

این به ما امکان می دهد رفتار سطوح و منحنی ها را در فضای سه بعدی مطالعه کنیم.

در حساب دیفرانسیل و انتگرال، بردار گرادیان برای تعریف مفهوم مشتق جهت دار استفاده می شود.

مشتق جهتی سرعت تغییر یک تابع در یک جهت خاص را اندازه گیری می کند.

با گرفتن حاصل ضرب نقطه ای بردار گرادیان و یک بردار واحد در جهت دلخواه، می توانیم مشتق جهت یک تابع را محاسبه کنیم.

به طور کلی، بردار گرادیان ابزار قدرتمندی در ریاضیات است که کاربردهای متعددی در زمینه های مختلف دارد.

این به ما کمک می کند تا مسائل بهینه سازی را حل کنیم، پدیده های فیزیکی را درک کنیم و رفتار سطوح و منحنی ها را مطالعه کنیم.

توانایی آن در ارائه اطلاعات در مورد جهت و میزان تغییرات آن را به یک مفهوم اساسی در بسیاری از رشته های ریاضی تبدیل می کند.

بنابراین، دفعه بعد که با مشکلی مواجه شدید که شامل یافتن حداکثر یا حداقل مقدار یک تابع یا درک رفتار یک فیلد برداری است، بردار گرادیان و کاربردهای آن را به خاطر بسپارید.

کاوش در خواص بردار گرادیان

بردار گرادیان یک مفهوم ریاضی است که نقش مهمی در حساب برداری ایفا می کند.

برداری است که در جهت شیب زیاد یک تابع در یک نقطه مشخص است.

به عبارت دیگر، جهتی را که یک تابع سریعترین افزایش می یابد به ما می گوید.

برای درک ویژگی های بردار گرادیان، ابتدا تابعی از دو متغیر f(x,y) را در نظر می گیریم.

بردار گرادیان این تابع با ∇f(x,y) نشان داده می شود، که در آن ∇ عملگر del است.

عملگر del یک عملگر دیفرانسیل برداری است که گرادیان را در فضای سه بعدی نشان می دهد.

بردار گرادیان دو ویژگی مهم دارد: جهت و قدر.

جهت بردار گرادیان همیشه بر منحنی های سطح تابع عمود است.

منحنی های سطح منحنی هایی روی یک نمودار هستند که نشان دهنده نقاطی هستند که تابع دارای مقدار ثابتی است.

بردار گرادیان در جهت تندترین افزایش تابع در یک نقطه معین از منحنی تراز است.

بزرگی بردار گرادیان نشان دهنده نرخ تغییر تابع در یک نقطه معین است.

هر چه اندازه بردار گرادیان بزرگتر باشد، افزایش تابع تندتر است.

برعکس، قدر کوچکتر نشان دهنده افزایش ملایم تر است.

برای محاسبه بردار گرادیان از مشتقات جزئی استفاده می کنیم.

برای تابع f(x,y)، بردار گرادیان با ∇f(x,y) = (∂f/∂x، ∂f/∂y) داده می شود.

مشتق جزئی با توجه به x (∂f/∂x) نشان دهنده نرخ تغییر تابع نسبت به x است، در حالی که مشتق جزئی با توجه به y (∂f/∂y) نشان دهنده نرخ تغییر نسبت به x است. y

توجه به این نکته ضروری است که بردار گرادیان، صرف نظر از ابعاد تابع، همیشه بر منحنی های سطح عمود است.

این ویژگی برای توابع سه یا چند متغیر نیز صادق است.

در ابعاد بالاتر، بردار گرادیان با عملگر del و تابعی مانند ∇f(x، y، z) نشان داده می شود.

بردار گرادیان در فیزیک و مهندسی نیز کاربرد دارد.

به عنوان مثال، در فیزیک، بردار گرادیان برای محاسبه میدان الکتریکی، میدان گرانشی و سایر میدان های برداری استفاده می شود.

در مهندسی برای بهینه سازی توابع و یافتن مقادیر حداکثر یا حداقل استفاده می شود.

در نتیجه، بردار گرادیان یک مفهوم اساسی در حساب برداری است که جهت و بزرگی شیب زیاد یک تابع را در یک نقطه معین نشان می دهد.

همیشه بر منحنی های سطح تابع عمود است و با استفاده از مشتقات جزئی قابل محاسبه است.

بردار گرادیان در زمینه های مختلف از جمله فیزیک و مهندسی کاربرد دارد.

درک خواص آن برای حل مسائل مربوط به توابع چندین متغیر ضروری است.

محاسبه بردار گرادیان در حساب چند متغیره

در حساب چند متغیره، یکی از مفاهیم اساسی بردار گرادیان است.

بردار گرادیان برداری است که در جهت تندترین افزایش یک تابع در یک نقطه مشخص است.

این یک ابزار ضروری برای درک رفتار توابع در ابعاد چندگانه است.

برای محاسبه بردار گرادیان، ابتدا باید مفهوم مشتقات جزئی را درک کنیم.

در حساب دیفرانسیل و انتگرال چند متغیره، توابع دارای چندین متغیر هستند و مشتقات جزئی به ما این امکان را می دهند که نرخ تغییر تابع را نسبت به هر متغیر به صورت جداگانه اندازه گیری کنیم، در حالی که متغیرهای دیگر را ثابت نگه داریم.

بردار گرادیان با گرفتن مشتقات جزئی یک تابع نسبت به هر متغیر و ترکیب آنها در یک بردار تشکیل می شود.

برای مثال، اگر تابع f(x,y) داشته باشیم، بردار گرادیان به صورت ∇f(x,y) یا grad(f(x,y)) نمایش داده می شود.

برای محاسبه بردار گرادیان، مشتق جزئی تابع را نسبت به متغیر اول x و سپس مشتق جزئی را نسبت به متغیر دوم y می گیریم.

سپس این مشتقات جزئی در یک بردار ترکیب می شوند که مشتق جزئی با توجه به x به عنوان جزء اول و مشتق جزئی با توجه به y به عنوان جزء دوم است.

بردار گرادیان اطلاعات ارزشمندی در مورد رفتار یک تابع ارائه می دهد.

جهت آن نشان دهنده جهت تندترین افزایش تابع در یک نقطه معین است.

اگر تابع را به صورت سطح تصور کنیم، بردار گرادیان در جهت تندترین شیب سربالایی است.

بزرگی بردار گرادیان نشان دهنده نرخ تغییر تابع در آن جهت است.

قدر بزرگتر نشان دهنده شیب تندتر است، در حالی که قدر کوچکتر نشان دهنده شیب ملایمتر است.

با تجزیه و تحلیل بردار گرادیان، می توانیم جهت و سرعت تغییر یک تابع را در هر نقطه مشخص تعیین کنیم.

بردار گرادیان ویژگی مهم دیگری نیز دارد: همیشه بر منحنی های سطح تابع عمود است.

منحنی های سطح منحنی هایی روی سطح تابع هستند که نشان دهنده نقاطی هستند که تابع دارای مقدار ثابتی است.

بردار گرادیان همیشه بر این منحنی ها عمود است زیرا در جهت تندترین افزایش است که عمود بر منحنی های تراز است.

این ویژگی بردار گرادیان به ما امکان می دهد خطوط مماس بر منحنی های تراز را پیدا کنیم.

با گرفتن حاصل ضرب نقطه ای بردار گرادیان و یک بردار مماس بر منحنی تراز، می توانیم شیب خط مماس را تعیین کنیم.

این یک ابزار مفید برای درک رفتار توابع و منحنی سطح آنها است.

در نتیجه، بردار گرادیان یک مفهوم اساسی در حساب دیفرانسیل و انتگرال چند متغیره است.

با گرفتن مشتقات جزئی یک تابع نسبت به هر متغیر و ترکیب آنها در یک بردار تشکیل می شود.

بردار گرادیان اطلاعاتی در مورد جهت و سرعت تغییر یک تابع در یک نقطه معین و همچنین عمود بر منحنی های تراز ارائه می دهد.

درک بردار گرادیان برای تحلیل رفتار توابع در ابعاد چندگانه ضروری است.

تجسم بردار گرادیان در فیلدهای برداری

بردار گرادیان چیست؟ ? خوب، برای درک این مفهوم، باید به دنیای فیلدهای برداری بپردازیم.

فیلدهای برداری اشیایی ریاضی هستند که به هر نقطه از فضا یک بردار اختصاص می دهند.

این بردارها جهت و بزرگی برخی از کمیت های فیزیکی مانند سرعت یا نیرو را نشان می دهند.

آنها معمولا در فیزیک، مهندسی و گرافیک کامپیوتری برای مدل سازی و تجزیه و تحلیل پدیده های مختلف استفاده می شوند.

حال، بیایید روی تجسم بردار گرادیان در فیلدهای برداری تمرکز کنیم.

بردار گرادیان یک مفهوم اساسی در حساب برداری است که به ما کمک می کند رفتار یک میدان اسکالر را درک کنیم.

یک فیلد اسکالر، بر خلاف یک فیلد برداری، یک مقدار اسکالر به هر نقطه از فضا اختصاص می دهد.

نمونه هایی از میدان های اسکالر عبارتند از دما، فشار و غلظت.

بردار گرادیان یک میدان اسکالر برداری است که در جهت تندترین افزایش میدان اسکالر در یک نقطه مشخص است.

به عبارت دیگر، جهتی را که میدان اسکالر سریعترین تغییر را در آن دارد به ما می گوید.

بزرگی بردار گرادیان نشان دهنده نرخ تغییر میدان اسکالر در آن جهت است.

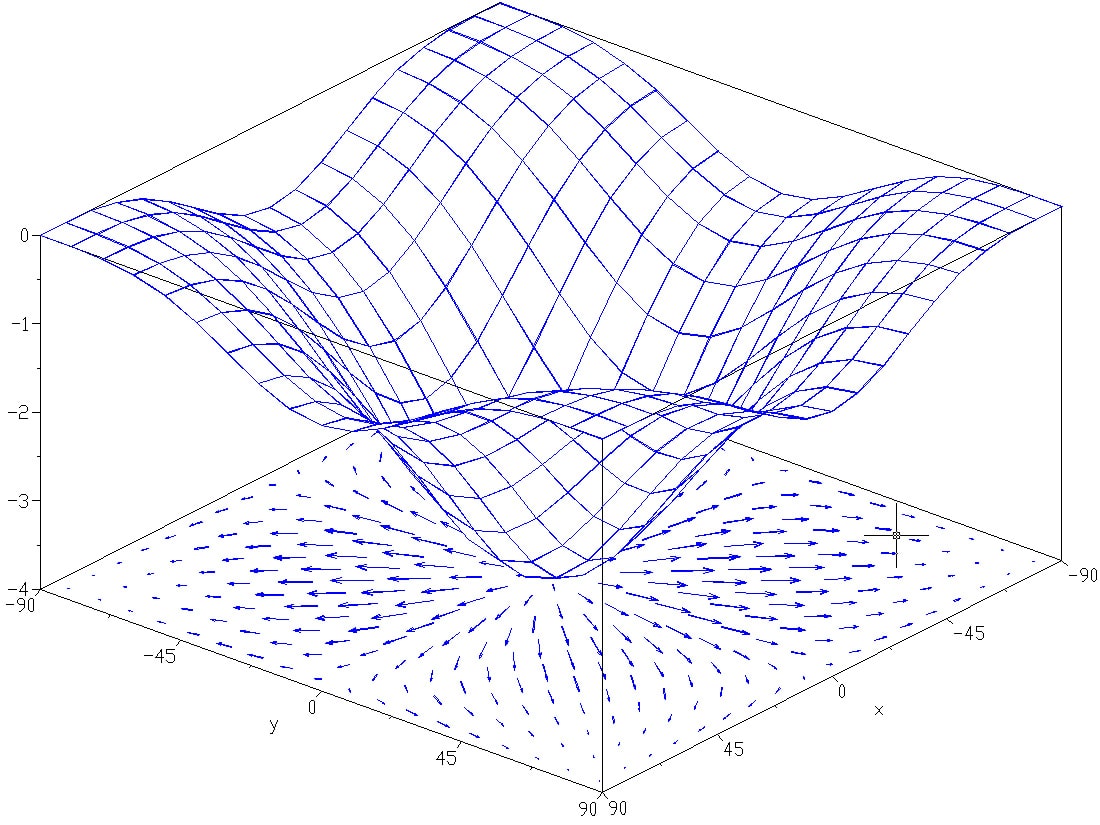
برای تجسم بردار گرادیان، می‌توانیم یک فلش کوچک را در هر نقطه از میدان اسکالر قرار دهیم.

جهت پیکان مربوط به جهت بردار گرادیان است، در حالی که طول فلش نشان دهنده بزرگی بردار گرادیان است.

با قرار دادن این فلش ها در هر نقطه از میدان اسکالر، می توانیم یک نمایش بصری از میدان بردار گرادیان ایجاد کنیم.

حال بیایید مثالی را برای درک بهتر نحوه عملکرد بردار گرادیان در نظر بگیریم.

یک میدان اسکالر دو بعدی را تصور کنید که توزیع دما را در یک اتاق نشان می دهد.

دما در نزدیکی بخاری بالاتر است و با دور شدن از آن کاهش می یابد.

برای تجسم میدان بردار گرادیان، فلش‌هایی را به سمت گرم‌کننده قرار می‌دهیم، با فلش‌های بلندتر که کاهش سریع‌تر دما را نشان می‌دهد.

میدان بردار گرادیان می تواند بینش های ارزشمندی در مورد رفتار میدان های اسکالر ارائه دهد.

به عنوان مثال، می تواند به ما کمک کند مناطقی را که دارای تغییرات سریع هستند شناسایی کنیم یا نقاطی را با مقادیر حداکثر یا حداقل تعیین کنیم.

با تجزیه و تحلیل میدان بردار گرادیان، می توانیم درک عمیق تری از میدان اسکالر زیربنایی به دست آوریم و بر اساس این دانش تصمیمات آگاهانه بگیریم.

علاوه بر تجسم میدان بردار گرادیان، می توانیم اجزای آن را نیز محاسبه کنیم.

در فضای دو بعدی، بردار گرادیان دو جزء دارد: یکی در جهت x و دیگری در جهت y.

این مولفه ها را می توان با استفاده از مشتقات جزئی محاسبه کرد که میزان تغییر میدان اسکالر را با توجه به هر مختصات اندازه گیری می کند.

در نتیجه، بردار گرادیان ابزار قدرتمندی برای تجسم و تحلیل میدان‌های اسکالر است.

با نشان دادن جهت و بزرگی شیب زیاد یک میدان اسکالر در هر نقطه، بینش های ارزشمندی را در مورد رفتار میدان ارائه می دهد.

میدان بردار گرادیان به ما کمک می‌کند تا پدیده‌های پیچیده را درک کنیم.

بنابراین، دفعه بعد که با یک میدان اسکالر مواجه شدید، فراموش نکنید که میدان بردار گرادیان آن را تجسم کنید و اسرار پنهان آن را باز کنید.

منبع » آکادمی اشکان مستوفی