کورولیشن یا همبستگی در یادگیری ماشین

درک ضرایب همبستگی یا کورولیشن در یادگیری ماشین بسیار مهم است زیرا آنها به ما کمک می کنند تا قدرت و جهت رابطه بین دو متغیر را تعیین کنیم. این دانش می تواند به طور قابل توجهی بر عملکرد و قابلیت تفسیر مدل های یادگیری ماشین شما تأثیر بگذارد.

بنابراین، بیایید تجزیه کنیم که ضرایب همبستگی چیست و چرا در یادگیری ماشین اهمیت دارند.

کورولیشن یا همبستگی در یادگیری ماشین

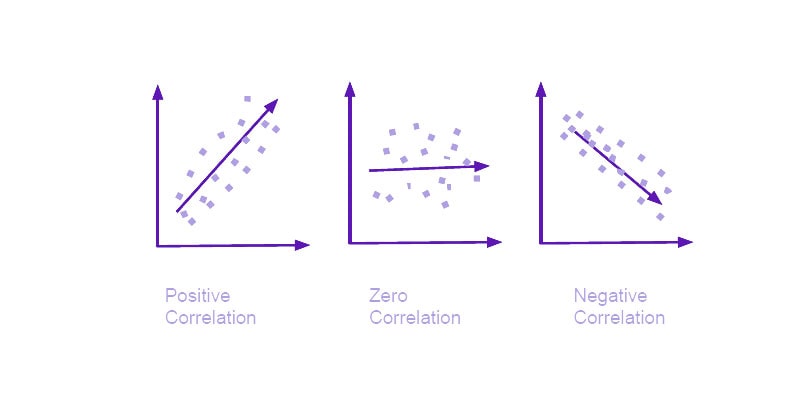
اول از همه، ضرایب همبستگی مقادیر عددی هستند که از 1- تا 1 متغیر هستند.

این مقادیر نشان می‌دهند که دو متغیر چقدر با هم مرتبط هستند.

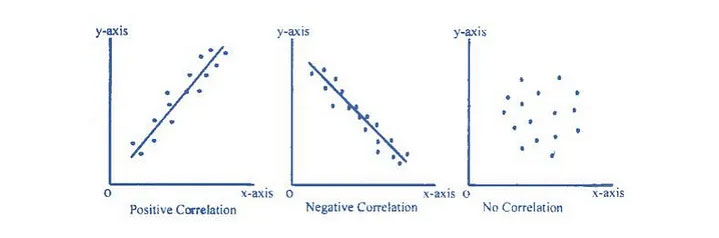
ضریب همبستگی 1 به این معنی است که یک رابطه مثبت کامل وجود دارد، به این معنی که با افزایش یک متغیر، متغیر دیگر نیز افزایش می یابد.

برعکس، ضریب همبستگی 1- نشان دهنده یک رابطه منفی کامل است که در آن یک متغیر با کاهش متغیر دیگر افزایش می یابد.

مقدار 0 هیچ رابطه ای را نشان نمی دهد.

روابط در کورولیشن یا همبستگی

به عنوان مثال، اگر روی یک مشکل رگرسیون کار می کنید، دانستن اینکه کدام ویژگی با متغیر هدف شما همبستگی بالایی دارد می تواند به شما کمک کند مرتبط ترین ویژگی ها را برای مدل خود انتخاب کنید.

این می تواند منجر به عملکرد بهتر و پیش بینی های دقیق تر شود.

از طرف دیگر، اگر دو ویژگی بسیار با یکدیگر همبستگی دارند، ممکن است ایده خوبی باشد که یکی از آنها را کنار بگذارید تا از چند خطی بودن جلوگیری کنید، که می تواند مدل شما را پایدارتر کند و تفسیر آن را دشوارتر کند.

اکنون، ممکن است تعجب کنید که چگونه این ضرایب همبستگی را محاسبه کنید.

محاسبه ضرایب کورولیشن یا همبستگی

رایج ترین روش ضریب همبستگی پیرسون است که رابطه خطی بین دو متغیر را اندازه گیری می کند.

با این حال، شایان ذکر است که همبستگی پیرسون فقط روابط خطی را نشان می دهد.

اگر داده های شما یک رابطه غیر خطی دارند، ممکن است بخواهید روش های دیگری مانند همبستگی رتبه اسپیرمن یا تاو کندال را در نظر بگیرید.

هنگامی که ضرایب همبستگی را محاسبه کردید، مرحله بعدی تفسیر آنها است.

اینجاست که همه چیز ممکن است کمی پیچیده شود.

همبستگی بالا لزوماً به معنای علیت نیست.

فقط به این دلیل که دو متغیر با هم مرتبط هستند به این معنی نیست که یکی باعث تغییر دیگری می شود.

به عنوان مثال، فروش بستنی و حوادث غرق شدن ممکن است ارتباط زیادی با هم داشته باشند، اما این بدان معنا نیست که خرید بستنی باعث غرق شدن می شود.

در عوض، هر دو احتمالاً تحت تأثیر یک متغیر سوم، مانند هوای گرم هستند.

درک این تفاوت های ظریف برای تصمیم گیری آگاهانه در پروژه های یادگیری ماشین شما ضروری است.

برای مثال، اگر در حال ساخت یک مدل پیش‌بینی برای قیمت سهام هستید، ممکن است متوجه شوید که شاخص‌های اقتصادی خاصی با قیمت سهام همبستگی بالایی دارند.

با این حال، گنجاندن کورکورانه این شاخص ها در مدل خود بدون درک روابط اساسی می تواند منجر به نتایج گمراه کننده شود.

علاوه بر این، ضرایب همبستگی نیز می تواند در مهندسی ویژگی کمک کند.

با درک روابط بین ویژگی‌های مختلف، می‌توانید ویژگی‌های جدیدی ایجاد کنید که این روابط را به طور مؤثرتری ثبت کنید.

به عنوان مثال، اگر متوجه شدید که دو ویژگی با هم ارتباط زیادی دارند، ممکن است یک ویژگی جدید ایجاد کنید که آنها را به نحوی ترکیب کند که تأثیر مشترک آنها را بر متغیر هدف نشان دهد.

به طور خلاصه، ضرایب همبستگی یک ابزار قدرتمند در جعبه ابزار یادگیری ماشین هستند.

آنها به شما کمک می کنند تا روابط بین متغیرها را درک کنید، که می تواند انتخاب ویژگی، ساخت مدل و تفسیر را مشخص کند.

با این حال، مهم است که به یاد داشته باشید که همبستگی به معنای علیت نیست و در هنگام تفسیر این ارزش ها، زمینه وسیع تری را در نظر بگیرید.

با انجام این کار، برای ساختن مدل های یادگیری ماشینی قوی و دقیق مجهزتر خواهید شد.

چگونه در مدل های یادگیری ماشینی چند خطی بودن را مدیریت کنیم

وقتی با مدل‌های یادگیری ماشینی کار می‌کنید، چند خطی بودن می‌تواند یک سردرد واقعی باشد.

اساساً، زمانی اتفاق می‌افتد که دو یا چند متغیر پیش‌بینی‌کننده در یک مجموعه داده با هم مرتبط باشند، به این معنی که اطلاعات اضافی را ارائه می‌دهند.

این افزونگی می‌تواند با توانایی مدل برای تعیین اثر فردی هر پیش‌بینی‌کننده مشکل ایجاد کند، که منجر به نتایج کمتر قابل اعتماد و کمتر قابل تفسیر می‌شود.

بنابراین، چگونه چند خطی بودن را در مدل های یادگیری ماشینی خود مدیریت می کنید؟ بیایید به چند استراتژی عملی بپردازیم.

اول از همه، شناسایی چند خطی بودن قبل از پرداختن به آن بسیار مهم است.

یکی از روش های رایج محاسبه ماتریس همبستگی متغیرهای پیش بینی کننده شما است.

اگر هر جفت متغیری را با ضریب همبستگی بالا، مثلاً بالای 0.8 یا 0.

9 مشاهده کنید، ممکن است مشکل چند خطی داشته باشید.

ابزار مفید دیگر ضریب تورم واریانس (VIF) است.

مقدار VIF بیشتر از 10 اغلب نشان دهنده چند خطی بودن بالا در نظر گرفته می شود.

هنگامی که مقصران را شناسایی کردید، می توانید به نحوه برخورد با آنها فکر کنید.

یک رویکرد ساده حذف یکی از متغیرهای همبسته است.

این ممکن است کمی شدید به نظر برسد، اما اگر دو متغیر اساساً اطلاعات یکسانی را ارائه می دهند، حذف یکی به طور قابل توجهی به عملکرد مدل شما آسیب نمی رساند.

در واقع می تواند مدل شما را ساده تر و قابل تفسیرتر کند.

با این حال، این روش همیشه ایده آل نیست، به خصوص اگر هر دو متغیر برای تحلیل شما مهم باشند.

تکنیک دیگر ترکیب متغیرهای همبسته در یک ویژگی واحد است.

به عنوان مثال، می توانید میانگین یا مجموع دو متغیر را در نظر بگیرید.

به این ترتیب، شما اطلاعاتی را که آنها ارائه می کنند را بدون نیاز به اضافه کاری حفظ می کنید.

تجزیه و تحلیل اجزای اصلی (PCA) روش پیچیده تری برای دستیابی به این امر است.

PCA متغیرهای همبسته شما را به مجموعه‌ای از مؤلفه‌های غیرهمبسته تبدیل می‌کند که سپس می‌تواند به عنوان پیش‌بینی‌کننده در مدل شما استفاده شود.

این نه تنها به چند خطی بودن کمک می کند، بلکه می تواند ابعاد مجموعه داده شما را کاهش دهد و مدل شما را کارآمدتر کند.

روش‌های منظم‌سازی مانند رگرسیون ریج و رگرسیون کمند نیز در مدیریت چند خطی مؤثر هستند.

رگرسیون ریج یک جریمه به ضرایب رگرسیون اضافه می کند و آنها را به سمت صفر کاهش می دهد اما دقیقاً صفر نیست.

این می‌تواند با کاهش واریانس تخمین‌های ضرایب به کاهش تأثیر چند خطی کمک کند.

از سوی دیگر، رگرسیون کمند، در واقع می تواند برخی از ضرایب را صفر کند و به طور موثر انتخاب متغیر را انجام دهد.

هر دو روش می توانند ثبات و عملکرد مدل شما را در حضور چند خطی بهبود بخشند.

همچنین شایان ذکر است که گاهی اوقات، دانش دامنه می تواند بسیار ارزشمند باشد.

اگر روابط زیربنایی بین متغیرهای خود را درک کنید، ممکن است بتوانید تصمیمات آگاهانه تری در مورد اینکه کدام متغیرها را نگه دارید، ترکیب کنید یا تبدیل کنید، بگیرید.

برای مثال، اگر با داده‌های اقتصادی کار می‌کنید، ممکن است بدانید که شاخص‌های خاصی به طور طبیعی با هم مرتبط هستند و می‌توانند مدل شما را بر این اساس تنظیم کنند.

به طور خلاصه، در حالی که چند خطی می تواند مدل های یادگیری ماشین شما را پیچیده کند، استراتژی های متعددی برای مدیریت موثر آن وجود دارد.

فرقی نمی‌کند که متغیرها را حذف کنید، آنها را ترکیب کنید، از PCA استفاده کنید یا از تکنیک‌های منظم‌سازی استفاده کنید، نکته کلیدی این است که از مشکل آگاه باشید و اقدامات پیشگیرانه برای رسیدگی به آن انجام دهید.

با انجام این کار، نه تنها عملکرد مدل‌های خود را بهبود می‌بخشید، بلکه آنها را قابل تفسیر و قابل اعتمادتر می‌کنید.

بنابراین دفعه بعد که با چند خطی مواجه شدید، وحشت نکنید – فقط این نکات را به خاطر بسپارید و با آن مقابله کنید.

منبع » آکادمی اشکان مستوفی