رگرسیون معادله عادی رگرسیون معادله نرمال (Normal equation regression) چیست؟ اگر تا به حال وارد دنیای تحلیل رگرسیون شده باشید، ممکن است با اصطلاح «رگرسیون معادلات عادی» برخورد کرده باشید.
اما دقیقا به چه معناست؟ به بیان ساده، معادله نرمال یک فرمول ریاضی است که به ما امکان می دهد مقادیر بهینه ضرایب را در یک مدل رگرسیون خطی پیدا کنیم.
درک معادله نرمال در رگرسیون
این یک راه حل به شکل بسته ارائه می دهد، به این معنی که می توانیم مقادیر را مستقیماً بدون نیاز به الگوریتم های بهینه سازی تکراری محاسبه کنیم.
برای درک معادله نرمال، اجازه دهید ابتدا اصول رگرسیون خطی را دوباره مرور کنیم.
در این نوع تحلیل، هدف ما یافتن بهترین خطی است که نشان دهنده رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل است.
خط با شیب (ضریب) و قطع آن تعریف می شود.
هدف به حداقل رساندن مجموع مجذور اختلاف بین مقادیر مشاهده شده و مقادیر پیش بینی شده در خط است.
به طور سنتی، ما از روش حداقل مربعات برای تخمین ضرایب استفاده می کنیم.
این شامل به حداقل رساندن مجموع مجذور باقیمانده است که تفاوت بین مقادیر مشاهده شده و پیش بینی شده است.
در حالی که این روش به طور گسترده استفاده می شود و موثر است، برای یافتن ضرایب بهینه نیاز به الگوریتم های بهینه سازی تکراری دارد.
این می تواند از نظر محاسباتی گران باشد، به خصوص برای مجموعه داده های بزرگ.
اینجاست که معادله نرمال وارد می شود.
راهی برای محاسبه مستقیم ضرایب بهینه بدون نیاز به الگوریتم های تکراری ارائه می دهد.
فرمول معادله نرمال به صورت زیر است:
θ = (X^TX)^-1 X^T y
در اینجا θ نشان دهنده بردار ضرایب، X ماتریس متغیرهای مستقل، y بردار مقادیر مشاهده شده و (X^TX)^-1 نشان دهنده معکوس حاصلضرب ماتریس X^T و X است.
با استفاده از معادله نرمال می توانیم ضرایب بهینه را در یک مرحله پیدا کنیم.
این امر به ویژه هنگام برخورد با مجموعه داده های کوچک تا متوسط مفید است، زیرا هزینه محاسباتی در مقایسه با الگوریتم های بهینه سازی تکراری به طور قابل توجهی کاهش می یابد.
با این حال، توجه به این نکته مهم است که معادله نرمال محدودیت هایی دارد.
یکی از محدودیتهای اصلی این است که ماتریس (X^TX) باید معکوس باشد.
به عبارت دیگر، متغیرهای مستقل باید به صورت خطی مستقل باشند و نباید چند خطی کامل وجود داشته باشد.
اگر این شرایط برآورده نشود، نمی توان از معادله عادی استفاده کرد و روش های جایگزین مانند رگرسیون پشته یا رگرسیون کمند ممکن است مناسب تر باشد.
محدودیت دیگر این است که معادله نرمال می تواند به نقاط پرت در داده ها حساس باشد.
نقاط پرت می توانند تا حد زیادی بر ضرایب تخمین زده شده تأثیر بگذارند و منجر به پیش بینی های نادرست شوند.
بنابراین، بررسی دقیق دادهها برای نقاط پرت و در نظر گرفتن تکنیکهای رگرسیون قوی در صورت لزوم بسیار مهم است.
در نتیجه، معادله نرمال ابزار قدرتمندی در تحلیل رگرسیون است که به ما امکان می دهد ضرایب بهینه را در یک مدل رگرسیون خطی پیدا کنیم.
این یک راه حل شکل بسته ارائه می دهد و نیاز به الگوریتم های بهینه سازی تکراری را از بین می برد.
با این حال، محدودیت های خود را دارد و ممکن است برای همه شرایط مناسب نباشد.
درک معادله نرمال و مفروضات آن برای تحلیل رگرسیون دقیق و قابل اعتماد ضروری است.
مزایا و محدودیت های رگرسیون معادله نرمال
نرمال رگرسیون معادله یک روش رایج است که در آمار و یادگیری ماشین برای یافتن بهترین خط مناسب برای مجموعه دادهای از نقاط داده استفاده میشود.
این یک رویکرد ساده و سرراست است که هم مزایا و هم محدودیت هایی دارد.
یکی از مزایای اصلی رگرسیون معادلات نرمال، سادگی آن است.
برخلاف سایر روشهای رگرسیون که به الگوریتمهای بهینهسازی تکراری نیاز دارند، رگرسیون معادله معمولی یک راهحل بسته ارائه میکند.
این بدان معنی است که شما می توانید مستقیماً ضرایب بهترین خط را بدون نیاز به هیچ روش تکراری محاسبه کنید.
این سادگی، رگرسیون معادله معمولی را از نظر محاسباتی کارآمد و آسان برای پیاده سازی می کند.
مزیت دیگر رگرسیون معادله عادی این است که تخمین های بی طرفانه ضرایب را ارائه می دهد.
به عبارت دیگر، ضرایب به دست آمده از رگرسیون معادلات نرمال تحت تأثیر هیچ گونه خطای نمونه گیری یا سوگیری در داده ها قرار نمی گیرند.
این به این دلیل است که رگرسیون معادله نرمال مجموع مربعات خطاها را به حداقل می رساند، که معیاری برای اختلاف بین نقاط داده مشاهده شده و مقادیر پیش بینی شده است.
با به حداقل رساندن این خطا، رگرسیون معادله نرمال تضمین می کند که ضرایب بدون هیچ گونه سوگیری تخمین زده می شوند.
علاوه بر این، رگرسیون معادله نرمال می تواند چندین متغیر مستقل را مدیریت کند.
بر خلاف رگرسیون خطی ساده که فقط یک متغیر مستقل را در نظر می گیرد، رگرسیون معادله عادی می تواند چندین متغیر مستقل را به طور همزمان در خود جای دهد.
این آن را به ابزاری همه کاره برای تجزیه و تحلیل مجموعه داده های پیچیده با پیش بینی کننده های متعدد تبدیل می کند.
با این حال، رگرسیون معادله نرمال نیز محدودیت های خود را دارد.
یک محدودیت این است که می تواند به موارد پرت حساس باشد.
نقاط پرت نقاط داده ای هستند که به طور قابل توجهی از الگوی کلی داده ها انحراف دارند.
از آنجایی که رگرسیون معادله نرمال مجموع مجذور خطاها را به حداقل می رساند، نقاط پرت می توانند تأثیر نامتناسبی بر ضرایب برآورد شده داشته باشند.
این بدان معنی است که اگر مجموعه داده شما حاوی مقادیر پرت باشد، بهترین خط به دست آمده از رگرسیون معادله معمولی ممکن است رابطه اساسی بین متغیرها را به درستی نشان ندهد.
یکی دیگر از محدودیت های رگرسیون معادله عادی این است که می تواند از نظر محاسباتی برای مجموعه داده های بزرگ گران باشد.
راه حل شکل بسته رگرسیون معادله عادی شامل معکوس کردن یک ماتریس است که می تواند برای مجموعه داده هایی با تعداد زیادی مشاهدات زمان بر و حافظه فشرده باشد.
در چنین مواردی، روشهای رگرسیون جایگزین که از الگوریتمهای بهینهسازی تکراری استفاده میکنند ممکن است مناسبتر باشند.
در نتیجه، رگرسیون معادله نرمال یک روش ساده و کارآمد برای یافتن بهترین خط مناسب برای مجموعه دادهای از نقاط داده است.
تخمین های بی طرفانه ای از ضرایب ارائه می دهد و می تواند چندین متغیر مستقل را مدیریت کند.
با این حال، برای مجموعه دادههای بزرگ میتواند به موارد پرت حساس باشد و از نظر محاسباتی گران باشد.
بنابراین، هنگام انتخاب روش رگرسیون برای تحلیل، مهم است که مزایا و محدودیتهای رگرسیون معادلات عادی را در نظر بگیرید.
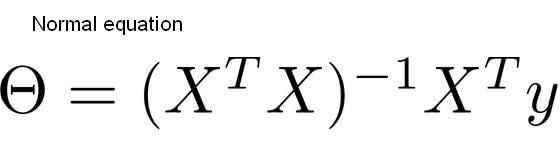
مقایسه نرمال رگرسیون معادله با سایر تکنیک های رگرسیون
رگرسیون معادلات عادی یک تکنیک رایج است که در آمار و یادگیری ماشین برای پیش بینی رابطه بین متغیرها استفاده می شود.
اغلب برای تعیین مزایا و معایب آن با سایر تکنیک های رگرسیون مقایسه می شود.
در این مقاله، چگونگی مقایسه رگرسیون معادله معمولی با سایر تکنیکهای رگرسیون و اینکه چرا یک ابزار ارزشمند در تجزیه و تحلیل دادهها است را بررسی خواهیم کرد.
یکی از مزایای اصلی رگرسیون معادلات نرمال، سادگی آن است.
برخلاف سایر تکنیکهای رگرسیون که به الگوریتمهای بهینهسازی تکراری نیاز دارند، رگرسیون معادله معمولی یک راهحل بسته ارائه میکند.
این بدان معناست که میتوانیم مستقیماً مقادیر بهینه ضرایب رگرسیون را بدون نیاز به روشهای بهینهسازی پیچیده محاسبه کنیم.
این سادگی، رگرسیون معادله معمولی را از نظر محاسباتی کارآمد و آسان برای پیاده سازی می کند.
مزیت دیگر رگرسیون معادلات عادی توانایی آن در مدیریت مجموعه داده های بزرگ است.
برخی از تکنیکهای رگرسیون، مانند نزول گرادیان، میتوانند از نظر محاسباتی گران باشند که با تعداد زیادی مشاهدات سروکار دارند.
از سوی دیگر، رگرسیون معادله عادی، میتواند به طور موثر مجموعههای داده بزرگ را بدون کاهش دقت مدیریت کند.
این باعث می شود آن را به یک انتخاب ترجیحی برای تجزیه و تحلیل داده های بزرگ تبدیل کند.
رگرسیون معادله نرمال علاوه بر سادگی و مقیاس پذیری، تخمین های بی طرفانه ای از ضرایب رگرسیون ارائه می دهد.
این بدان معنی است که ضرایب برآورد شده به طور متوسط با ضرایب واقعی جمعیت برابر است.
این ویژگی به ویژه هنگام استنباط در مورد رابطه بین متغیرها مهم است.
با ارائه تخمینهای بیطرفانه، رگرسیون معادلات عادی به ما امکان میدهد تا بر اساس دادههای نمونه خود، نتایج معتبری در مورد جامعه بگیریم.
با این حال، رگرسیون معادله نرمال در مقایسه با سایر تکنیک های رگرسیون دارای محدودیت هایی است.
یک محدودیت این است که فرض می کند رابطه بین متغیرها خطی است.
اگر رابطه غیر خطی باشد، رگرسیون معادله نرمال ممکن است الگوی زیربنایی را به دقت نشان ندهد.
در چنین مواردی، سایر تکنیک های رگرسیون، مانند رگرسیون چند جمله ای یا رگرسیون غیر خطی، ممکن است مناسب تر باشند.
یکی دیگر از محدودیت های رگرسیون معادله نرمال، حساسیت آن به چند خطی است.
چند خطی زمانی رخ می دهد که دو یا چند متغیر پیش بینی با یکدیگر همبستگی زیادی داشته باشند.
در چنین مواردی، رگرسیون معادله نرمال ممکن است برآوردهای ناپایداری از ضرایب رگرسیون ایجاد کند.
برای پرداختن به این موضوع، سایر تکنیکهای رگرسیون، مانند رگرسیون پشته یا رگرسیون کمند، میتوانند برای کاهش اثرات چند خطی استفاده شوند.
علیرغم این محدودیت ها، رگرسیون معادله نرمال یک ابزار ارزشمند در تجزیه و تحلیل داده ها باقی مانده است.
سادگی، مقیاس پذیری و بی طرفی آن، آن را به یک انتخاب محبوب برای بسیاری از برنامه ها تبدیل کرده است.
علاوه بر این، رگرسیون معادله نرمال به عنوان پایه ای برای تکنیک های رگرسیون پیشرفته تر عمل می کند و یک نقطه شروع محکم برای تجزیه و تحلیل بیشتر فراهم می کند.
در نتیجه، رگرسیون معادله نرمال یک تکنیک قدرتمند برای پیشبینی رابطه بین متغیرها است.
این سادگی، مقیاس پذیری و بی طرفی را ارائه می دهد و آن را به ابزاری ارزشمند در تجزیه و تحلیل داده ها تبدیل می کند.
در حالی که ممکن است در مدیریت روابط غیر خطی و چند خطی بودن محدودیت هایی داشته باشد، رگرسیون معادله عادی به عنوان یک پایه محکم برای تکنیک های رگرسیون پیشرفته تر عمل می کند.
با درک نقاط قوت و ضعف رگرسیون معادلات عادی، محققان و تحلیلگران می توانند تصمیمات آگاهانه ای در مورد اینکه کدام تکنیک رگرسیون را در تحلیل خاص خود استفاده کنند، اتخاذ کنند.
کاربردهای واقعی رگرسیون معادله عادی
رگرسیون معادلات عادی ابزار قدرتمندی است که در آمار و یادگیری ماشین برای یافتن بهترین خط مناسب برای مجموعه دادهای از نقاط داده استفاده میشود.
این روشی است که به ما امکان می دهد تا رابطه بین دو متغیر را تخمین بزنیم و بر اساس آن رابطه پیش بینی کنیم.
در حالی که ممکن است پیچیده به نظر برسد، رگرسیون معادله عادی کاربردهای متعددی در دنیای واقعی دارد که به راحتی قابل درک است.
یکی از رایج ترین کاربردهای رگرسیون معادلات عادی در حوزه مالی است.
تحلیلگران مالی اغلب از این روش برای پیش بینی قیمت سهام بر اساس داده های تاریخی استفاده می کنند.
با تجزیه و تحلیل رابطه بین عوامل مختلف مانند عملکرد شرکت، روند بازار و شاخص های اقتصادی، تحلیلگران می توانند پیش بینی های آگاهانه ای در مورد قیمت سهام در آینده انجام دهند.
این اطلاعات برای سرمایه گذارانی که می خواهند آگاهانه در مورد خرید یا فروش سهام تصمیم بگیرند بسیار ارزشمند است.
حوزه دیگری که در آن رگرسیون معادلات عادی به طور گسترده ای مورد استفاده قرار می گیرد، حوزه بازاریابی است.
شرکتها معمولاً حجم زیادی از دادهها را در مورد رفتار مشتری جمعآوری میکنند، مانند تاریخچه خرید، آمار جمعیتی و الگوهای مرور آنلاین.
با اعمال رگرسیون معادله نرمال برای این داده ها، بازاریابان می توانند بینشی در مورد ترجیحات مشتری به دست آورند و استراتژی های بازاریابی خود را بر اساس آن تنظیم کنند.
به عنوان مثال، یک شرکت ممکن است از تحلیل رگرسیون استفاده کند تا مشخص کند کدام کانال های تبلیغاتی در دستیابی به مخاطبان هدف خود مؤثرتر هستند و به آنها اجازه می دهد بودجه بازاریابی خود را به طور مؤثرتری تخصیص دهند.
از رگرسیون معادلات نرمال نیز در حوزه بهداشت و درمان استفاده می شود.
محققان پزشکی اغلب دادههایی را در مورد عوامل مختلفی مانند جمعیت شناسی بیمار، انتخاب سبک زندگی و سابقه پزشکی جمعآوری میکنند تا رابطه بین این عوامل و پیامدهای سلامتی را مطالعه کنند.
با اعمال رگرسیون معادله نرمال برای این داده ها، محققان می توانند عوامل خطر بیماری های خاص را شناسایی کرده و مداخلات هدفمندی را برای پیشگیری یا درمان آنها ایجاد کنند.
به عنوان مثال، یک مطالعه ممکن است از تجزیه و تحلیل رگرسیون برای تعیین رابطه بین سیگار کشیدن و سرطان ریه استفاده کند، و به مقامات بهداشت عمومی اجازه می دهد تا کمپین های ضد سیگار را توسعه دهند که در کاهش بروز این بیماری کشنده موثرتر است.
علاوه بر این کاربردهای خاص، رگرسیون معادلات عادی نیز به طور گسترده در زمینه هایی مانند اقتصاد، علوم اجتماعی و مهندسی استفاده می شود.
اقتصاددانان از تحلیل رگرسیون برای مطالعه رابطه بین متغیرهای مختلف اقتصادی مانند تولید ناخالص داخلی و نرخ بیکاری برای درک عواملی که باعث رشد اقتصادی می شوند استفاده می کنند.
دانشمندان علوم اجتماعی از تحلیل رگرسیون برای مطالعه رابطه بین متغیرهایی مانند سطح تحصیلات و درآمد استفاده میکنند تا عوامل مؤثر در نابرابری اجتماعی را درک کنند.
مهندسان از تحلیل رگرسیون برای مطالعه رابطه بین عوامل مختلف مانند دما، فشار و خواص مواد استفاده میکنند تا سیستمهای کارآمدتر و قابل اعتمادتری طراحی کنند.
در نتیجه، رگرسیون معادلات عادی یک ابزار همه کاره با کاربردهای متعدد در دنیای واقعی است.
از امور مالی تا بازاریابی، مراقبت های بهداشتی تا مهندسی، این روش به ما امکان می دهد داده ها را تجزیه و تحلیل کنیم و بر اساس رابطه بین متغیرها پیش بینی کنیم.
با درک کاربردهای رگرسیون معادلات عادی، می توانیم از قدرت آن برای به دست آوردن بینش، تصمیم گیری آگاهانه و هدایت نوآوری در زمینه های مختلف استفاده کنیم.
بنابراین، دفعه بعد که با مشکلی مواجه شدید که شامل تجزیه و تحلیل دادهها و انجام پیشبینی میشود، استفاده از رگرسیون معادلات عادی را به عنوان روش اصلی خود در نظر بگیرید.
منبع » آکادمی اشکان مستوفی