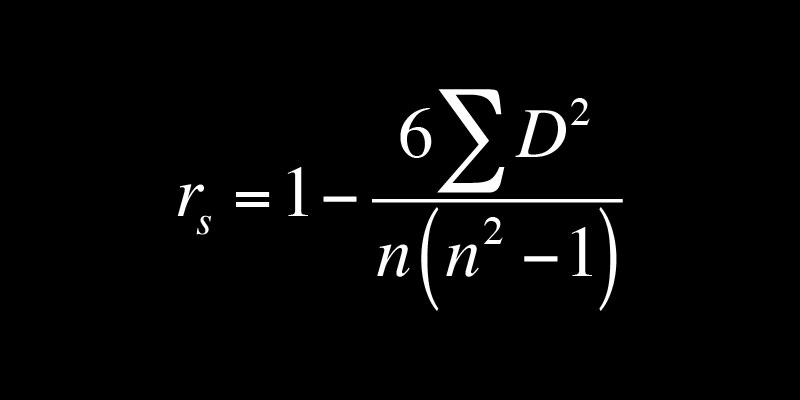ضریب همبستگی رتبهای اسپیرمن یا spearman’s rank correlation coefficient یک مفهوم مهم در زمینه یادگیری ماشین است که به تحلیل رابطه بین دو متغیر کمک میکند.
این ضریب، معیاری است که نشان میدهد که چقدر دو متغیر با یکدیگر همبستگی دارند، اما به جای اندازهگیری همبستگی خطی، از رتبههای دادهها استفاده میکند که در آکادمی اشکان مستوفی به آن خواهیم پرداخت.
ضریب همبستگی رتبهای اسپیرمن یا spearman’s rank correlation coefficient
برای محاسبه ضریب همبستگی رتبهای اسپیرمن، ابتدا باید دادهها را به ترتیب صعودی یا نزولی مرتب کنیم.
سپس برای هر جفت داده، رتبه آنها را محاسبه میکنیم.
سپس با استفاده از فرمولهای خاص، ضریب همبستگی رتبهای اسپیرمن را محاسبه میکنیم که مقادیر آن بین -1 تا 1 متغیر است.
ضریب همبستگی رتبهای اسپیرمن مفید است زیرا حساسیت کمتری نسبت به دادههای پرت دارد و میتواند روابط غیرخطی را نیز تشخیص دهد.
این ابزار مفیدی برای تحلیل دادههایی است که توزیع آنها ناهمگن است یا دارای دادههای پرت است.
در کل، ضریب همبستگی رتبهای اسپیرمن یک ابزار قدرتمند است که به ما کمک میکند تا روابط پیچیدهتر بین دادهها را در دادههایمان شناسایی کنیم و از آنها برای پیشبینی و تحلیل استفاده کنیم.
کاربردهای ضریب همبستگی رتبهای اسپیرمن در یادگیری ماشین
یکی از کاربردهای اصلی ضریب همبستگی رتبهای اسپیرمن در یادگیری ماشین، ارزیابی روابط غیرخطی بین ویژگیها و خروجیها است.
در بسیاری از مسائل واقعی، روابط بین ویژگیها و خروجیها ممکن است پیچیده و غیرخطی باشند و در این حالت استفاده از ضریب همبستگی رتبهای اسپیرمن میتواند به ما کمک کند تا این روابط را بهتر درک کنیم.
ضریب همبستگی رتبهای اسپیرمن همچنین میتواند در فرایند انتخاب ویژگیها در مدلهای یادگیری ماشین مفید باشد.
با استفاده از این ضریب، میتوانیم ویژگیهایی که بیشترین تأثیر را بر خروجی دارند را شناسایی کرده و از آنها برای ساخت مدلهای بهتر استفاده کنیم.
در مجموع، ضریب همبستگی رتبهای اسپیرمن یک ابزار قدرتمند در یادگیری ماشین است که به ما کمک میکند تا روابط پیچیده بین ویژگیها و خروجیها را درک کرده و مدلهای بهتری بسازیم.
از این رو، استفاده از این ابزار میتواند به بهبود عملکرد و دقت مدلهای یادگیری ماشین کمک کند.
مقایسه ضریب همبستگی رتبهای اسپیرمن با ضریب همبستگی پیرسون
این ضریب، میزان همبستگی بین دو متغیر را بر اساس رتبههای آنها اندازهگیری میکند، به عبارت دیگر، اگر دو متغیر رتبهای باشند، این ضریب نشان میدهد که چقدر تغییر در یک متغیر باعث تغییر در متغیر دیگر میشود.
اما برای درک بهتر این مفهوم، مقایسه آن با ضریب همبستگی پیرسون میتواند مفید باشد.
ضریب همبستگی پیرسون نیز برای اندازهگیری رابطه بین دو متغیر استفاده میشود، اما با این تفاوت که این ضریب بر اساس میزان تغییرات خطی بین دو متغیر اندازهگیری میشود.
به عبارت دیگر، اگر دو متغیر دارای توزیع نرمال باشند، ضریب همبستگی پیرسون بهترین اندازهگیری برای رابطه آنها است.
با این حال، ضریب همبستگی رتبهای اسپیرمن مزایای خود را دارد.
این ضریب، در مواردی که دادهها دارای توزیع غیر نرمال هستند یا دادهها دارای دادههای پرتی میباشند، بهترین گزینه برای اندازهگیری رابطه بین دو متغیر است.
همچنین، ضریب همبستگی رتبهای اسپیرمن، برای دادههای کمیتی و کیفیتی نیز قابل استفاده است.
در نهایت، بیشتر محققان و دادهکاوان در حوزه یادگیری ماشین به طور گسترده از ضریب همبستگی رتبهای اسپیرمن استفاده میکنند تا روابط پیچیدهتر بین دادهها را بررسی کنند.
این ضریب، ابزار موثری برای تحلیل دادههای غیر خطی و غیر نرمال است و میتواند به تحلیل دقیقتر و صحیحتر دادهها کمک کند.
روشهای محاسبه ضریب همبستگی رتبهای اسپیرمن
برای محاسبه ضریب همبستگی رتبهای اسپیرمن، ابتدا باید دادهها را به ترتیب از کم به زیاد یا از زیاد به کم مرتب کنیم.
سپس برای هر زوج داده، رتبه آنها را مشخص میکنیم.
سپس با استفاده از فرمول محاسبه ضریب همبستگی اسپیرمن، مقدار آن را محاسبه میکنیم.
ضریب همبستگی رتبهای اسپیرمن مقادیری بین -1 و 1 دارد.
اگر این ضریب برابر با 1 باشد، این نشان دهنده یک رابطه مثبت کامل بین دو متغیر است.
اگر این ضریب برابر با -1 باشد، این نشان دهنده یک رابطه منفی کامل بین دو متغیر است.
و اگر این ضریب برابر با صفر باشد، این نشان دهنده عدم وجود هرگونه رابطه بین دو متغیر است.
استفاده از ضریب همبستگی رتبهای اسپیرمن در یادگیری ماشین میتواند به ما کمک کند تا ارتباط بین ویژگیهای مختلف دادهها را درک کنیم و الگوریتمهای بهتری برای پیشبینی و تحلیل دادهها ایجاد کنیم.
این روش میتواند به ما کمک کند تا الگوریتمهای دقیقتری برای مسائل پیچیدهتری مانند پیشبینی قیمتها یا تحلیل تصاویر ارائه دهیم.
بنابراین، استفاده از ضریب همبستگی رتبهای اسپیرمن یک ابزار مهم در دستهبندی و پیشبینی دادهها در زمینه یادگیری ماشین است که میتواند به ما کمک کند تا الگوریتمهای بهتری برای حل مسائل پیچیده ارائه دهیم.
مزایا و معایب استفاده از ضریب همبستگی رتبهای اسپیرمن در مسائل یادگیری ماشین
یکی از مزایای استفاده از این ضریب این است که برای دادههایی که توزیع آنها ناهمگن است، مناسب است.
به عبارت دیگر، این ضریب برای دادههایی که توزیع آنها نرمال نیست، بهترین گزینه است.
یکی از مزایای دیگر استفاده از ضریب همبستگی رتبهای اسپیرمن این است که از تاثیر دادههای پرت بر روی نتایج کاسته میشود.
این به این معنی است که اگر دادههای شما دارای پرتی باشند، این ضریب به شما کمک میکند تا رابطه واقعی بین دو متغیر را بدون تحت تاثیر قرار گرفتن از دادههای پرت بررسی کنید.
اما همانطور که همیشه، استفاده از هر ابزاری همراه با معایب خود است.
یکی از معایب استفاده از ضریب همبستگی رتبهای اسپیرمن این است که این ضریب برای دادههای کمیتی مناسب نیست و تنها برای دادههای رتبهای مناسب است.
بنابراین، اگر دادههای شما به صورت کمیتی هستند، بهتر است از روشهای دیگری برای بررسی رابطه بین دو متغیر استفاده کنید.
در نهایت، استفاده از ضریب همبستگی رتبهای اسپیرمن در مسائل یادگیری ماشین میتواند به شما کمک کند تا رابطه بین دو متغیر را بررسی کنید و از تاثیر دادههای پرت کاسته شود.
اما باید به این نکته توجه داشت که این روش تنها برای دادههای رتبهای مناسب است و برای دادههای کمیتی مناسب نیست.
منبع » آکادمی اشکان مستوفی