ضریب همبستگی پیرسون یا pearson correlation coefficient یکی از مفاهیم مهم در حوزه یادگیری ماشین است که برای اندازهگیری رابطه بین دو متغیر استفاده میشود.
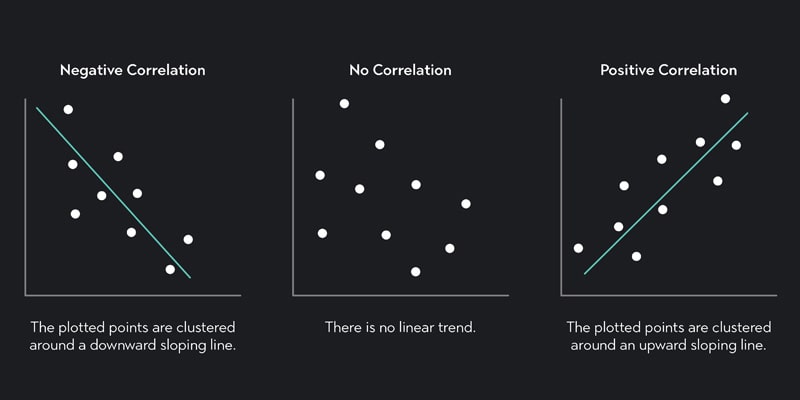
این ضریب از -1 تا 1 مقادیر میگیرد که نشاندهنده قدرت و جهت رابطه بین دو متغیر است.
اگر ضریب همبستگی برابر با 1 باشد، این نشاندهنده یک رابطه خطی مثبت بین دو متغیر است، به این معنی که هرچه یک متغیر افزایش یابد، متغیر دیگر نیز افزایش خواهد یافت.
از سوی دیگر، اگر ضریب همبستگی برابر با -1 باشد، این نشاندهنده یک رابطه خطی منفی بین دو متغیر است، به این معنی که هرچه یک متغیر افزایش یابد، متغیر دیگر کاهش خواهد یافت.
ضریب همبستگی پیرسون در یادگیری ماشین
در یادگیری ماشین، استفاده از ضریب همبستگی پیرسون برای اندازهگیری رابطه بین ویژگیهای ورودی و خروجی مدل بسیار مفید است.
اگر ضریب همبستگی بین یک ویژگی و خروجی مدل مثبت باشد، این نشاندهنده این است که افزایش یا کاهش در ویژگی مورد نظر، تاثیر مثبت یا منفی بر روی خروجی دارد.
از این رو، میتوان از ضریب همبستگی برای انتخاب ویژگیهای مهم و حذف ویژگیهای غیرمفید استفاده کرد.
به عنوان مثال، در یک مسئله پیشبینی قیمت خانه، میتوان از ضریب همبستگی برای اندازهگیری رابطه بین ویژگیهایی مانند متراژ، تعداد اتاقها، موقعیت و قیمت خانه استفاده کرد.
اگر ضریب همبستگی بین متراژ و قیمت مثبت باشد، این نشاندهنده این است که افزایش متراژ خانه، باعث افزایش قیمت آن میشود.
در نهایت، ضریب همبستگی پیرسون یک ابزار قدرتمند برای تحلیل دادهها و انتخاب ویژگیهای مهم در یادگیری ماشین است.
با استفاده از این ابزار، میتوان بهترین ویژگیها را برای ساخت مدلهای دقیقتر و کارآمدتر انتخاب کرد و عملکرد مدل را بهبود بخشید.
روشهای محاسبهٔ ضریب همبستگی پیرسون در مدلهای یادگیری ماشین
برای محاسبه ضریب همبستگی پیرسون بین دو متغیر، ابتدا باید میانگین هر متغیر را محاسبه کرده و سپس اختلاف هر مقدار از میانگین متغیرها را محاسبه کنیم.
سپس این اختلافات را با یکدیگر ضرب کرده و مجموع آنها را محاسبه میکنیم.
در نهایت، این مقدار را بر تعداد نمونهها کاهش داده و بر تفاوت استاندارد دو متغیر تقسیم میکنیم تا به ضریب همبستگی پیرسون برسیم.
ضریب همبستگی پیرسون میتواند به عنوان یک ابزار مفید برای تحلیل دادهها و پیشبینی رفتارهای آینده استفاده شود.
این ضریب در بسیاری از مدلهای یادگیری ماشین، از جمله رگرسیون خطی و شبکههای عصبی، به کار میرود تا رابطه بین ورودیها و خروجیها را بررسی کند و به ما کمک کند تا مدلهای بهتری بسازیم.
در مجموع، ضریب همبستگی پیرسون یک ابزار قدرتمند است که به ما کمک میکند تا روابط پیچیدهای را در دادهها شناسایی کرده و بهبود درک ما از رفتار دادهها و پدیدههای مختلف را فراهم کند.
این ابزار اساسی برای تحلیل دادهها و ساخت مدلهای پیشبینی در حوزه یادگیری ماشین است و بدون آن، امکان تحلیل و استفاده از دادهها به صورت بهینه واقع نمیشود.
کاربردهای ضریب همبستگی پیرسون در پیشبینی و تحلیل دادهها
با استفاده از این ضریب، میتوان ارتباط بین ویژگیهای مختلف یک داده را بررسی کرد و از آن برای پیشبینی مقادیر ناشناخته استفاده کرد.
به عنوان مثال، در یادگیری ماشین، میتوان از ضریب همبستگی برای پیشبینی قیمت یک محصول بر اساس ویژگیهای مختلف آن استفاده کرد.
ضریب همبستگی پیرسون همچنین در تحلیل دادهها نیز کاربرد دارد.
با استفاده از این ضریب، میتوان ارتباط بین دادههای مختلف را بررسی کرد و الگوهای مختلف را شناسایی کرد.
این اطلاعات میتواند به تصمیمگیریهای مهم در حوزههای مختلف کمک کند و به بهبود عملکرد سیستمها کمک کند.
به طور کلی، ضریب همبستگی پیرسون یک ابزار قدرتمند در تحلیل دادهها و پیشبینیها است که به ما کمک میکند تا الگوهای مختلف را شناسایی کرده و از آنها برای بهبود فرآیندهای مختلف استفاده کنیم.
این ابزار اساسی در حوزه یادگیری ماشین است و برای تحلیل دادههای پیچیده و پیشبینیهای دقیق بسیار مفید است.
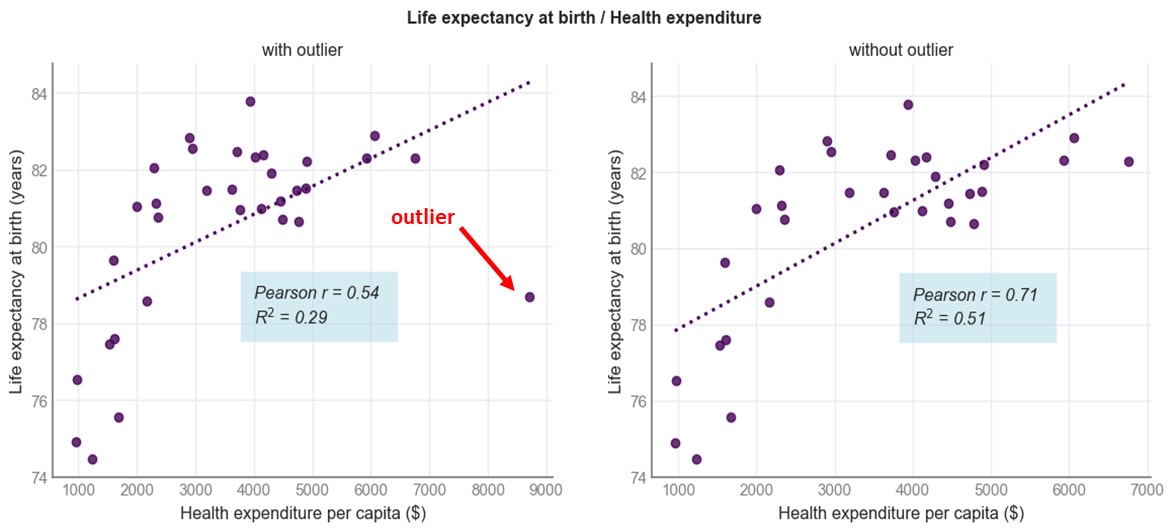
تفاوتها بین ضریب همبستگی پیرسون و سایر معیارهای همبستگی در یادگیری ماشین
اگر ضریب همبستگی برابر با 1 باشد، این نشاندهنده یک رابطه خطی مثبت بین دو متغیر است، در حالی که اگر برابر با -1 باشد، این نشاندهنده یک رابطه خطی منفی است.
اما اگر ضریب همبستگی برابر با صفر باشد، این نشاندهنده عدم وجود هرگونه رابطه خطی بین دو متغیر است.
ضریب همبستگی پیرسون از سایر معیارهای همبستگی مانند ضریب همبستگی Spearman و Kendall متمایز است.
ضریب همبستگی Spearman بر اساس رتبههای دادهها محاسبه میشود و برای دادههایی که توزیع آنها نرمال نیست مناسب است.
اما ضریب همبستگی Kendall بر اساس تطابق رتبهها محاسبه میشود و برای دادههایی که دارای پرتی است مناسب است.
ضریب همبستگی پیرسون به دلیل سادگی محاسبه و تفسیر آسان آن، یکی از معیارهای محبوب در یادگیری ماشین است.
با این حال، باید توجه داشت که این معیار تنها قادر به تشخیص روابط خطی بین دو متغیر است و ممکن است برای دادههای غیرخطی مناسب نباشد.
در نهایت، استفاده از ضریب همبستگی پیرسون در یادگیری ماشین بستگی به نوع دادهها و مسئله مورد نظر دارد.
برای دادههای خطی و روابط خطی، ضریب همبستگی پیرسون مناسب است، اما برای دادههای غیرخطی بهتر است از معیارهای همبستگی دیگر استفاده کرد.
نکات مهم در تفسیر و استفاده از ضریب همبستگی پیرسون در مسائل یادگیری ماشین
استفاده از ضریب همبستگی پیرسون در مسائل یادگیری ماشین میتواند به تحلیل دادهها و پیشبینی مقادیر آینده کمک کند.
با این حال، برای تفسیر صحیح این ضریب باید توجه به چند نکته مهم داشت.
اولین نکته این است که ضریب همبستگی پیرسون تنها قادر به تشخیص روابط خطی بین دو متغیر است و ممکن است روابط غیرخطی را نادیده بگیرد.
بنابراین، قبل از استفاده از این ضریب باید از صحت خطی بودن رابطه متغیرها اطمینان حاصل کرد.
در ادامه، باید به اندازهگیری قدرت رابطه بین دو متغیر توجه کرد.
اگر ضریب همبستگی نزدیک به 1 یا -1 باشد، این نشاندهنده وجود رابطه قوی بین دو متغیر است.
اما اگر این ارزش نزدیک به صفر باشد، این نشاندهنده وجود رابطه ضعیف یا عدم وجود رابطه است.
همچنین، باید به اهمیت اندازه نمونهها در تفسیر ضریب همبستگی توجه کرد.
با افزایش تعداد نمونهها، قدرت تخمین ضریب همبستگی افزایش مییابد و اطمینان از صحت آن افزایش مییابد.
در نهایت، باید به احتمال وقوع خطاهای تصادفی در تفسیر ضریب همبستگی توجه کرد.
برای اطمینان از صحت نتایج، میتوان از روشهای آماری دیگر همچون بازه اطمینان استفاده کرد.
با رعایت این نکات مهم، میتوان از ضریب همبستگی پیرسون به عنوان یک ابزار قدرتمند برای تحلیل دادهها و پیشبینی مقادیر آینده در مسائل یادگیری ماشین استفاده کرد.
منبع » آکادمی اشکان مستوفی