رگرسیون خطی (Linear regression) در یادگیری ماشین یک مفهوم اساسی در یادگیری ماشین است که به طور گسترده برای پیش بینی مقادیر عددی استفاده می شود. این یک الگوریتم ساده و در عین حال قدرتمند است که اساس مدل های پیچیده تر را تشکیل می دهد.
در این مقاله شما را با مفهوم رگرسیون خطی در یادگیری ماشین آشنا می کنیم و نحوه عملکرد آن را توضیح می دهیم.
مقدمه ای بر رگرسیون خطی در یادگیری ماشین
در هسته رگرسیون ، رگرسیون خطی یک رویکرد آماری برای مدلسازی رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل است.
هدف یافتن بهترین خطی است که رابطه بین این متغیرها را نشان می دهد. سپس می توان از این خط برای پیش بینی نقاط داده جدید استفاده کرد.
برای درک رگرسیون خطی، اجازه دهید یک مثال ساده را در نظر بگیریم.
فرض کنید مجموعه داده ای داریم که حاوی اطلاعاتی در مورد خانه ها، مانند اندازه و قیمت آنها است.
ما می توانیم از رگرسیون خطی برای ساخت مدلی استفاده کنیم که قیمت خانه را بر اساس اندازه آن پیش بینی کند.
در این حالت، اندازه خانه متغیر مستقل است که به عنوان متغیر پیش بینی نیز شناخته می شود، در حالی که قیمت، متغیر وابسته است که به عنوان متغیر هدف نیز شناخته می شود.
هدف یافتن یک معادله خطی به شکل y = mx + b است که در آن y نشان دهنده قیمت پیش بینی شده، x نشان دهنده اندازه خانه، m نشان دهنده شیب خط، و b نشان دهنده y-برق است.
برای یافتن بهترین خط مناسب، باید مقادیر m و b را تعیین کنیم که تفاوت بین قیمتهای پیشبینیشده و قیمتهای واقعی در مجموعه داده ما را به حداقل برساند.
این کار با به حداقل رساندن یک تابع هزینه، مانند میانگین مربعات خطا، که میانگین مجذور اختلاف بین مقادیر پیش بینی شده و واقعی را اندازه می گیرد، انجام می شود.
هنگامی که مدل رگرسیون خطی خود را آموزش دادیم، می توانیم از آن برای پیش بینی نقاط داده جدید استفاده کنیم.
به عنوان مثال، اگر اندازه یک خانه جدید داریم، می توانیم آن را به معادله خود وصل کنیم تا قیمت پیش بینی شده را بدست آوریم.
به خاطر داشته باشید که رگرسیون خطی یک رابطه خطی بین متغیرهای مستقل و وابسته را فرض می کند، بنابراین ممکن است برای مجموعه داده هایی با روابط پیچیده یا غیرخطی مناسب نباشد.
رگرسیون خطی همچنین می تواند برای مدیریت چندین متغیر مستقل که به عنوان رگرسیون خطی چندگانه شناخته می شود، گسترش یابد.
در این حالت، معادله تبدیل به y = b0 + b1x1 + b2x2 + … + bnxn می شود که b0 نشان دهنده نقطه ی y و b1، b2، …، bn نشان دهنده شیب خطوط برای هر متغیر مستقل است.
علاوه بر پیش بینی مقادیر عددی، از رگرسیون خطی می توان برای کارهای دیگر نیز استفاده کرد.
به عنوان مثال، می توان از آن برای انتخاب ویژگی استفاده کرد، جایی که ما مهم ترین متغیرهایی را تعیین می کنیم که به پیش بینی کمک می کنند.
همچنین میتوان از آن برای تشخیص پرت استفاده کرد، جایی که ما نقاط دادهای را شناسایی میکنیم که به طور قابلتوجهی از مقادیر پیشبینیشده انحراف دارند.
در نتیجه، رگرسیون خطی یک مفهوم اساسی در یادگیری ماشین است که به طور گسترده برای پیشبینی مقادیر عددی استفاده میشود.
این یک الگوریتم ساده و در عین حال قدرتمند است که اساس مدل های پیچیده تر را تشکیل می دهد.
با یافتن بهترین خطی که رابطه بین متغیرهای مستقل و وابسته را نشان میدهد، رگرسیون خطی به ما امکان میدهد در نقاط داده جدید پیشبینی کنیم.
میتوان آن را برای مدیریت چندین متغیر مستقل گسترش داد و میتواند برای کارهایی مانند انتخاب ویژگی و تشخیص موارد پرت استفاده شود.
درک ریاضیات پشت رگرسیون خطی
هدف از رگرسیون خطی یافتن بهترین خطی است که رابطه بین دو متغیر را نشان می دهد.
این متغیرها معمولاً به عنوان متغیر مستقل (X) و متغیر وابسته (Y) نامیده می شوند.
هدف یافتن خطی است که فاصله بین مقادیر پیش بینی شده و مقادیر واقعی را به حداقل برساند.
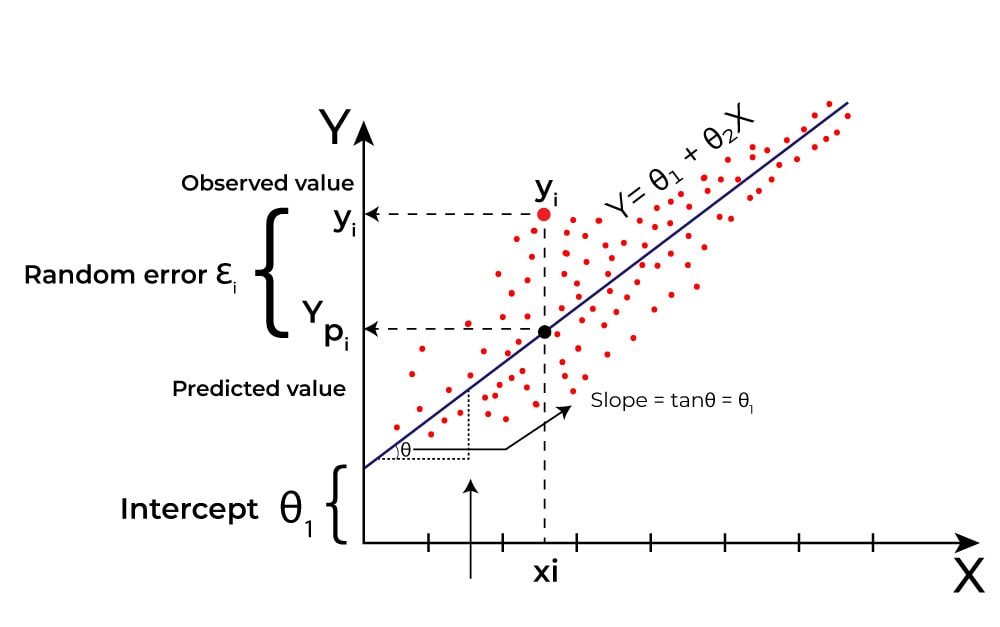
برای درک چگونگی عملکرد رگرسیون خطی، درک مفهوم معادله خطی مهم است.
در سادهترین شکل آن، یک معادله خطی را میتوان به صورت Y = mX + b نشان داد، که m شیب خط و b نقطه قطع y است.
شیب نشان دهنده نرخ تغییر Y نسبت به X است، در حالی که y-intercept مقدار Y است زمانی که X برابر با صفر است.
فرآیند یافتن بهترین خط برازش شامل تعیین مقادیر بهینه برای m و b است.
این کار با به حداقل رساندن مجموع اختلاف مجذور بین مقادیر پیش بینی شده و مقادیر واقعی انجام می شود.
این تکنیک به روش حداقل مربعات معروف است.
برای محاسبه شیب (m) و مقطع y (b)، میتوانیم از فرمولهای زیر استفاده کنیم:
m = (nΣXY – ΣXΣY) / (nΣX^2 – (ΣX)^2)
b = (ΣY – mΣX) / n
در اینجا n تعداد نقاط داده را نشان می دهد، ΣXY مجموع حاصلضرب های X و Y، ΣX مجموع مقادیر X و ΣY مجموع مقادیر Y است.
ΣX^2 مجموع مربعات مقادیر X را نشان می دهد.
هنگامی که مقادیر m و b را محاسبه کردیم، می توانیم از معادله خط برای پیش بینی استفاده کنیم.
با توجه به مقدار جدید X، میتوانیم آن را در معادله جایگزین کنیم تا مقدار پیشبینی شده مربوط به Y را بدست آوریم.
ذکر این نکته ضروری است که رگرسیون خطی یک رابطه خطی بین متغیرهای مستقل و وابسته را فرض می کند.
اگر رابطه خطی نباشد، پیشبینیها ممکن است دقیق نباشند.
در چنین مواردی، سایر الگوریتمهای یادگیری ماشین، مانند رگرسیون چند جملهای یا درختهای تصمیم، ممکن است مناسبتر باشند.
علاوه بر درک ریاضیات پشت رگرسیون خطی، ارزیابی عملکرد مدل نیز بسیار مهم است.
یکی از معیارهای رایج مورد استفاده برای این منظور، ضریب تعیین است که به عنوان R-squared نیز شناخته می شود.
R-squared نسبت واریانس در متغیر وابسته را اندازه گیری می کند که می تواند توسط متغیر(های) مستقل توضیح داده شود.
مقدار R-squared بالاتر نشان دهنده تناسب بهتر است.
در نتیجه، رگرسیون خطی یک الگوریتم یادگیری ماشین قدرتمند است که میتواند برای پیشبینی مقادیر پیوسته استفاده شود.
با درک ریاضیات زیربنایی، میتوانیم مفهوم یافتن بهترین خطی را که فاصله بین مقادیر پیشبینیشده و واقعی را به حداقل میرساند، درک کنیم.
مهم است که به یاد داشته باشید که رگرسیون خطی یک رابطه خطی بین متغیرها را فرض می کند و اینکه الگوریتم های دیگر ممکن است برای روابط غیر خطی مناسب تر باشند.
ارزیابی عملکرد مدل با استفاده از معیارهایی مانند R-squared می تواند به تعیین دقت پیش بینی ها کمک کند.
پیاده سازی رگرسیون خطی در پایتون برای یادگیری ماشین
رگرسیون خطی یک الگوریتم یادگیری ماشینی محبوب است که برای پیشبینی مقادیر عددی بر اساس مجموعهای از متغیرهای ورودی استفاده میشود.
این یک تکنیک ساده و در عین حال قدرتمند است که می تواند به راحتی در پایتون پیاده سازی شود.
در این مقاله نحوه پیاده سازی رگرسیون خطی در پایتون برای اهداف یادگیری ماشین را بررسی خواهیم کرد.
برای شروع، بیایید مفهوم اصلی رگرسیون خطی را درک کنیم.
این یک رویکرد آماری است که رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل را مدل می کند.
هدف یافتن بهترین خطی است که مجموع مجذور اختلاف بین مقادیر مشاهده شده و پیش بینی شده را به حداقل برساند.
پایتون چندین کتابخانه فراهم می کند که اجرای رگرسیون خطی را آسان می کند.
یکی از این کتابخانه ها scikit-learn است که به طور گسترده برای وظایف یادگیری ماشین استفاده می شود.
برای شروع، باید scikit-learn را با استفاده از pip، یک مدیریت بسته برای پایتون، نصب کنید.
هنگامی که scikit-learn را نصب کردید، می توانید ماژول های لازم را وارد کرده و مجموعه داده خود را بارگذاری کنید.
مجموعه داده باید در قالبی باشد که scikit-learn بتواند آن را درک کند، مانند یک فایل CSV.
می توانید از کتابخانه pandas برای خواندن فایل CSV و تبدیل آن به DataFrame استفاده کنید که یک ساختار داده با برچسب دو بعدی است.
پس از بارگذاری مجموعه داده، باید آن را به دو قسمت تقسیم کنید: متغیرهای ورودی (X) و متغیر هدف (y).
متغیرهای ورودی ویژگی هایی هستند که شما از آنها برای پیش بینی استفاده خواهید کرد، در حالی که متغیر هدف متغیری است که می خواهید پیش بینی کنید.
در رگرسیون خطی، متغیر هدف باید پیوسته باشد.
در مرحله بعد، باید مجموعه داده را به یک مجموعه آموزشی و یک مجموعه آزمایشی تقسیم کنید.
مجموعه آموزشی برای آموزش مدل رگرسیون خطی استفاده می شود، در حالی که مجموعه آزمون برای ارزیابی عملکرد آن استفاده می شود.
Scikit-learn یک تابع راحت به نام train_test_split ارائه می دهد که این کار را برای شما انجام می دهد.
هنگامی که مجموعه داده را تقسیم کردید، می توانید نمونه ای از مدل رگرسیون خطی ایجاد کنید و آن را با داده های آموزشی متناسب کنید.
برازش مدل به معنای یافتن بهترین خطی است که مجموع اختلاف مجذور بین مقادیر مشاهده شده و پیش بینی شده را به حداقل می رساند.
کلاس LinearRegression Scikit-learn یک روش مناسب ارائه می دهد که این کار را برای شما انجام می دهد.
پس از برازش مدل، می توانید با استفاده از روش پیش بینی، روی مجموعه تست پیش بینی کنید.
این به شما مجموعه ای از مقادیر پیش بینی شده برای متغیر هدف را می دهد.
سپس می توانید این مقادیر پیش بینی شده را با مقادیر واقعی در مجموعه آزمایشی برای ارزیابی عملکرد مدل مقایسه کنید.
برای ارزیابی عملکرد مدل رگرسیون خطی، می توانید از معیارهای مختلفی مانند میانگین مربعات خطا (MSE) و R-squared استفاده کنید.
MSE میانگین مجذور اختلاف بین مقادیر پیشبینیشده و واقعی را اندازهگیری میکند، در حالی که R-squared نسبت واریانس در متغیر هدف را که از متغیرهای ورودی قابل پیشبینی است، اندازهگیری میکند.
در نتیجه، اجرای رگرسیون خطی در پایتون برای اهداف یادگیری ماشین به لطف کتابخانه هایی مانند scikit-learn ساده است.
با دنبال کردن چند مرحله ساده، میتوانید یک مدل رگرسیون خطی را آموزش دهید، پیشبینی کنید و عملکرد آن را ارزیابی کنید.
رگرسیون خطی ابزار قدرتمندی است که می تواند در طیف وسیعی از کاربردها از پیش بینی قیمت مسکن گرفته تا تحلیل روندهای بازار سهام مورد استفاده قرار گیرد.
پس چرا آن را امتحان نکنید و ببینید چه بینش هایی را می توانید کشف کنید؟
ارزیابی و بهبود مدل های رگرسیون خطی
رگرسیون خطی یک روش محبوب است الگوریتم یادگیری ماشینی که برای پیشبینی مقادیر پیوسته استفاده میشود.
این ابزار ساده و در عین حال قدرتمندی است که می تواند برای تجزیه و تحلیل روابط بین متغیرها و پیش بینی بر اساس آن روابط مورد استفاده قرار گیرد.
با این حال، مانند هر مدل یادگیری ماشین دیگری، مدل های رگرسیون خطی کامل نیستند و می توانند از ارزیابی و بهبود بهره مند شوند.
یکی از راه های ارزیابی عملکرد مدل رگرسیون خطی، بررسی باقیمانده های آن است.
باقیمانده ها تفاوت بین مقادیر واقعی و مقادیر پیش بینی شده هستند.
با تجزیه و تحلیل باقیماندهها، میتوانیم تعیین کنیم که آیا مدل دارای خطاهای سیستماتیک است یا الگوهایی وجود دارد که مدل موفق به ثبت آن نشده است.
اگر باقیمانده ها یک الگوی تصادفی بدون روند واضح را نشان دهند، نشان دهنده عملکرد خوب مدل است.
از سوی دیگر، اگر الگوها یا روندهای واضحی در باقیمانده ها وجود داشته باشد، نشان می دهد که مدل تمام اطلاعات مربوطه را جمع آوری نمی کند و ممکن است نیاز به بهبود داشته باشد.
یکی دیگر از جنبه های مهم ارزیابی یک مدل رگرسیون خطی، ارزیابی خوب بودن برازش آن است.
خوب بودن برازش اندازهگیری میکند که مدل چقدر با دادهها مطابقت دارد.
یکی از معیارهای رایج مورد استفاده برای ارزیابی خوبی تناسب، مقدار مربع R است.
مقدار مربع R از 0 تا 1 متغیر است که 1 نشان دهنده تناسب کامل و 0 نشان دهنده عدم ارتباط بین متغیرها است.
یک مقدار R-squared بالا نشان می دهد که مدل بخش بزرگی از تغییرپذیری در داده ها را توضیح می دهد، در حالی که یک مقدار R-squared پایین نشان می دهد که مدل مقدار زیادی از تنوع را دریافت نمی کند.
هنگامی که عملکرد یک مدل رگرسیون خطی را ارزیابی کردیم، میتوانیم روی بهبود آن تمرکز کنیم.
یکی از راههای بهبود مدل رگرسیون خطی، افزودن ویژگیها یا متغیرهای بیشتر است.
با گنجاندن متغیرهای اضافی مرتبط با مشکل مورد نظر، به طور بالقوه میتوانیم اطلاعات بیشتری را به دست آوریم و قدرت پیشبینی مدل را بهبود ببخشیم.
با این حال، مهم است که هنگام اضافه کردن متغیرها احتیاط کنید، زیرا گنجاندن متغیرهای نامربوط یا اضافی در واقع می تواند عملکرد مدل را کاهش دهد.
روش دیگر برای بهبود مدل رگرسیون خطی، تبدیل متغیرها است.
گاهی اوقات، رابطه بین متغیرها و متغیر هدف ممکن است خطی نباشد.
در چنین مواردی، میتوانیم تبدیلهایی را به متغیرها اعمال کنیم تا رابطه را خطیتر کنیم.
تبدیل های رایج شامل گرفتن لگاریتم یا جذر متغیرها است.
با تبدیل متغیرها، میتوانیم به طور بالقوه برازش و دقت پیشبینی مدل را بهبود ببخشیم.
منظم سازی تکنیک دیگری است که می تواند برای بهبود مدل های رگرسیون خطی استفاده شود.
منظمسازی به جلوگیری از برازش بیش از حد کمک میکند، که زمانی اتفاق میافتد که مدل روی دادههای آموزشی به خوبی عمل کند اما نتواند به دادههای جدید و نادیده تعمیم یابد.
منظمسازی با افزودن یک عبارت جریمه به تابع هزینه مدل به این امر دست مییابد، که مدل را از اعطای اهمیت بیش از حد به هر یک از متغیرها منصرف میکند.
این به جلوگیری از پیچیده شدن بیش از حد مدل و تطبیق بیش از حد داده های آموزشی کمک می کند.
در نتیجه، ارزیابی و بهبود مدلهای رگرسیون خطی گام مهمی در فرآیند یادگیری ماشین است.
با تجزیه و تحلیل باقیماندهها، ارزیابی خوب بودن تناسب، و انجام بهبودهای لازم مانند افزودن متغیرها، تبدیل متغیرها یا اعمال منظمسازی، میتوانیم عملکرد مدل را افزایش دهیم و پیشبینیهای دقیقتری انجام دهیم.
رگرسیون خطی ممکن است یک الگوریتم ساده باشد، اما با ارزیابی دقیق و بهبود، می تواند ابزار قدرتمندی برای حل مسائل دنیای واقعی باشد.
کاربردهای واقعی رگرسیون خطی در یادگیری ماشین
رگرسیون خطی یک الگوریتم یادگیری ماشینی محبوب است که به طور گسترده در برنامه های مختلف دنیای واقعی استفاده می شود.
این یک تکنیک ساده و در عین حال قدرتمند است که به ما امکان می دهد یک متغیر خروجی پیوسته را بر اساس یک یا چند متغیر ورودی پیش بینی کنیم.
در این مقاله، برخی از کاربردهای واقعی رگرسیون خطی در یادگیری ماشین را بررسی خواهیم کرد.
یکی از رایج ترین کاربردهای رگرسیون خطی در حوزه مالی است.
موسسات مالی اغلب از رگرسیون خطی برای پیش بینی قیمت سهام، نرخ ارز و سایر شاخص های مالی استفاده می کنند.
با تجزیه و تحلیل داده های تاریخی، مدل های رگرسیون خطی می توانند الگوها و روندهایی را شناسایی کنند که به سرمایه گذاران در تصمیم گیری آگاهانه کمک می کند.
برای مثال می توان از مدل رگرسیون خطی برای پیش بینی قیمت آتی یک سهم بر اساس عملکرد تاریخی و سایر عوامل مرتبط استفاده کرد.
حوزه دیگری که در آن رگرسیون خطی کاربرد گسترده ای پیدا می کند در حوزه بازاریابی است.
شرکت ها از رگرسیون خطی برای تجزیه و تحلیل داده های مشتری و پیش بینی رفتار مصرف کننده استفاده می کنند.
با درک رابطه بین متغیرهای مختلف بازاریابی و فروش، کسب و کارها می توانند استراتژی های بازاریابی خود را بهینه کنند.
به عنوان مثال، یک شرکت می تواند از رگرسیون خطی برای تعیین تأثیر مخارج تبلیغاتی بر فروش و تخصیص بودجه بازاریابی خود استفاده کند.
رگرسیون خطی نیز به طور گسترده در زمینه مراقبت های بهداشتی استفاده می شود.
می توان از آن برای پیش بینی نتایج بیمار بر اساس عوامل مختلف پزشکی استفاده کرد.
برای مثال، یک مدل رگرسیون خطی را می توان بر روی مجموعه داده ای از سوابق بیمار آموزش داد تا احتمال ابتلای بیمار به بیماری خاصی را بر اساس سن، جنسیت و سایر عوامل مرتبط پیش بینی کند.
این اطلاعات می تواند به متخصصان مراقبت های بهداشتی در انجام مداخلات اولیه و بهبود مراقبت از بیمار کمک کند.
علاوه بر امور مالی، بازاریابی و مراقبت های بهداشتی، رگرسیون خطی در حوزه های دیگری مانند تجزیه و تحلیل ورزشی نیز استفاده می شود.
تیم های ورزشی از رگرسیون خطی برای تجزیه و تحلیل عملکرد بازیکنان و پیش بینی نتایج آینده استفاده می کنند.
با تجزیه و تحلیل داده های تاریخی، تیم ها می توانند شاخص های کلیدی عملکرد را شناسایی کرده و تصمیمات مبتنی بر داده را اتخاذ کنند.
به عنوان مثال، یک تیم بیسبال می تواند از رگرسیون خطی برای پیش بینی میانگین ضربات بازیکن بر اساس عملکرد قبلی و سایر عوامل مرتبط استفاده کند.
از رگرسیون خطی نیز در علوم محیطی برای تحلیل و پیشبینی عوامل مختلف محیطی استفاده میشود.
به عنوان مثال، می توان از آن برای پیش بینی تأثیر تغییرات آب و هوا بر سطح دریا، دما و سایر متغیرهای محیطی استفاده کرد.
با تجزیه و تحلیل داده های تاریخی، دانشمندان می توانند مدل هایی ایجاد کنند که به آنها در درک و کاهش اثرات تغییرات آب و هوایی کمک کند.
در نتیجه، رگرسیون خطی یک الگوریتم یادگیری ماشینی همه کاره است که کاربردها را در سناریوهای مختلف دنیای واقعی پیدا میکند.
از امور مالی گرفته تا بازاریابی، مراقبت های بهداشتی تا تجزیه و تحلیل ورزشی و علوم محیطی، رگرسیون خطی به ما کمک می کند تا پیش بینی ها و تصمیم گیری های آگاهانه را بر اساس داده های تاریخی انجام دهیم.
سادگی و تفسیرپذیری آن، آن را به انتخابی محبوب برای بسیاری از وظایف یادگیری ماشین تبدیل کرده است.
با ادامه پیشرفت فناوری، رگرسیون خطی احتمالاً یک ابزار ارزشمند در زمینه یادگیری ماشین باقی خواهد ماند.
منبع » آکادمی اشکان مستوفی